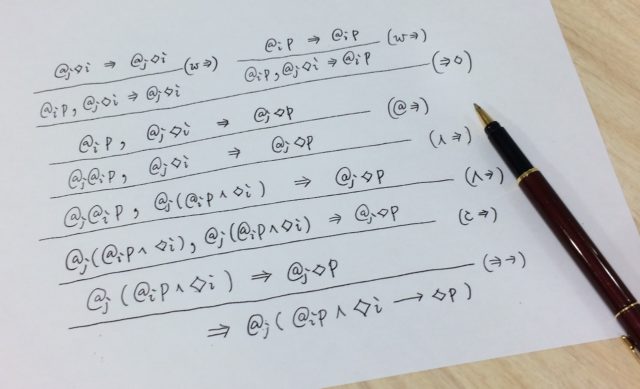Profile

- Research Subject
My research area is non-classical logics (in particular, modal logic) and their application. I am also interested in semantics of interrogatives (especially, inquisitive semantics), logical analyisis of puzzles on agents’ knowledge and belief, and history of logic (especially, Alan Turing’s thought).
- Research Fields
- Logic
- Faculty - Division / Research Group / Laboratory
- Division of Humanities / Research Group of Philosophy and Religious Studies / Laboratory of Philosophy and Ethics
- Graduate School - Division / Department / Laboratory
- Division of Humanities / Department of Philosophy and Religious Studies / Laboratory of Philosophy and Ethics
- School - Course / Laboratory
- Division of Humanities and Human Sciences / Course of Philosophy and Cultural Studies / Laboratory of Philosophy and Ethics
- Contact
Office/Lab: 603
Email: v-sano(at)let.hokudai.ac.jp
Replace “(at)” with “@” when sending email.Foreign exchange students who want to be research students (including Japanese residents) should apply for the designated period in accordance with the “Research Student Application Guidelines”. Even if you send an email directly to the staff, there is no reply.- Related Links
Lab.letters

Modal logic that delineates the world
through various combinations of “◇” and “□”
Logic, first systematized by the philosopher Aristotle, refers to a study that aims at the accurate and thorough delineation of the world. Various philosophers have taken their own approaches to addressing the challenging issue of how they should describe the world.
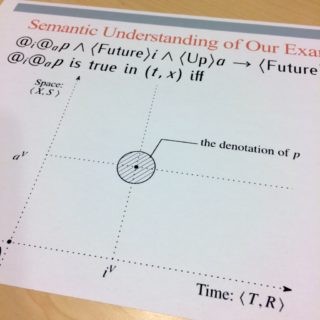
I have been interested in modal logic that addresses possibility and necessity of a proposition p, as represented symbolically by the expressions “◇p” (i.e., “It is possible that p.”) and “□p” (i.e., “It is necessary that p.”). While it is natural to relativize the truth of the possibility and necessity of p in terms of states or possible worlds, we may also relativize the truth of a given statement to several factors or domains, such as time, space, and agent. Each such relativization gives rise to new readings for ◇ and □. I have been involved in research on combining several readings of ◇ and □. I am currently investigating what results will follow from applying logic to social networking services such as Facebook.
Aim for infragile formalizations and proofs,
with a smooth connection between symbols and meanings.
At Hokkaido University, logic lectures are held annually in the undergraduate and graduate programs, which show that the university regards this subject as important. As a logician, I am delighted to conduct research in this excellent environment.
To study logic effectively, it is essential to practice writing proofs on paper. I would like my students to acquire the habit of checking whether symbols and their meanings are smoothly linked to each other by writing them down on paper. As Professor Kei Chiba, who is my former colleague in the Philosophy
and Ethics Laboratory at Hokkaido University, says, “It’s important to write infrangible sentences.” I second his slogan, and I would like to help you foster your research so that you can obtain infrangible
formalizations and proofs!
Message
“[I]t is not really difficult to construct a series of inferences, each dependent upon its predecessor and each simple in itself. If, after doing so, one simply knocks out all the central inferences and presents one’s audience with the starting-point and the conclusion, one may produce a startling, though possibly a meretricious, effect.” Even if each step is clear and trivial, the whole inference can be surprising. This is what Sherlock Homes explained as inferences in “ The Adventure of the Dancing Men’’ by Sir Arthur Conan Doyle, but some researcher cites this as a definition of logic. To put it the other way around, it is also a task of logic to reduce the surprising total into indecomposable trivial steps. In this respect, logic has only a few things that are trivial (things taken for granted), which is one of the appeals of this discipline. Moreover, accumulating inferences one by one has helped to settle down the idea of modern computers and further to identify problems that cannot be solved by any computers.
To learn logic, it is crucial to actually use your pen and paper to write up proofs and to construct counterexamples for the unproven. Seminars in our laboratory provide a lot of opportunities for students to learn how to write proofs, to construct counterexamples, and to explain the underlying ideas of proofs and counterexamples clearly and analytically to others. To publish obtained results of logic absolutely requires the skill of writing papers in English. In the master’s program, you can also hone your skills to author papers in English with the aim of presenting at international academic conferences. If you are interested in decomposing the surprising whole reasoning into indecomposable trivial steps, you are most welcome to knock on the door of logic!